Eksponen seringkali digunakan oleh para peneliti untuk memudahkan dalam menulis angka. Misalnya, ada seorang peneliti luar angkasa yang sedang melakukan pengukuran jarak antara Bumi dengan Mars. Kamu tahu kan seberapa jauh jaraknya? Ya, jaraknya berjuta-juta kilometer.
Nah supaya mudah dalam menulisnya, maka para peneliti menggunakan eksponen. Jadi, jarak yang berjuta-juta tadi, oleh peneliti ditulis dalam bentuk eksponen. Nah seperti apa sih eksponen itu? Yuk, simak penjelasannya di bawah ini.
Apa itu Eksponen?
Sebenarnya, materi eksponen ini sudah kamu pelajari di kelas 9 tahun lalu, lho! Hayoo, apa kamu masih ingat, apa yang dimaksud dengan eksponen? Eksponen adalah suatu bentuk perkalian dengan bilangan yang sama kemudian di ulang-ulang, yaa semacam perkalian yang diulang-ulang gitu deh.
Nah, kamu tahu nggak nih, siapa sih yang menemukan konsep eksponen itu? Jadi, konsep eksponen dalam matematika, pertama kali ditemukan oleh Rene Decartes, seorang filsuf dan matematikawan asal Prancis. Tujuan eksponen ini adalah untuk menyederhanakan atau mempersingkat penulisan perkalian bilangan yang sama, yaitu dalam bentuk pangkat.
Oleh karena itulah, eksponen bisa juga kita kenal sebagai bilangan berpangkat. Sebenarnya, memahami eksponen nggak cukup hanya hafal masalah perkalian saja, kamu juga harus memahami sifat-sifat dan bentuk lainnya dalam eksponen. Oke, sebelum kita ketahui apa saja sifat-sifat eksponen itu, ayo kita ketahui dulu bentuk umum eksponen. Yuk, simak baik-baik!

Oke, dalam memahami eksponen kita harus mengetahui terlebih dahulu sifat-sifat eksponen itu sendiri. Sifat-sifat eksponen sangat penting karena memiliki peran utama dalam dunia perpangkatan. Sekarang kita lihat ya seperti apa sifat-sifatnya.
Sifat-Sifat Eksponen
Ada beberapa sifat yang bisa kamu ketahui dalam memahami eksponen, di antaranya:
1. Pangkat Penjumlahan
am . an = am + n (perkalian eksponen dengan basis yang sama, maka pangkatnya harus ditambah)
Contoh: 42 . 43 = 42 + 3 = 45
2. Pangkat Pengurangan
am : an = am – n (pembagian eksponen dengan basis yang sama, maka pangkatnya harus dikurang)
Contoh: 45 : 43 = 45 – 3 = 42
3. Pangkat Perkalian
(am)n = am x n (jika bilangan berpangkat dipangkatkan lagi, maka pangkatnya harus dikali)
Contoh: (42)3 = 42 x 3 = 46
4. Perkalian Bilangan yang Dipangkatkan
(a . b)m = am . bm (perkalian bilangan yang dipangkatkan, maka masing-masing bilangan tersebut dipangkatkan juga)
Contoh: (3. 5)2 = 32. 52
5) Perpangkatan pada Bilangan Pecahan
Untuk bilangan pecahan yang dipangkatkan, maka bilangan pembilang dan penyebutnya harus dipangkatkan semua, dengan syarat nilai “b” atau penyebutnya tidak boleh sama dengan 0.
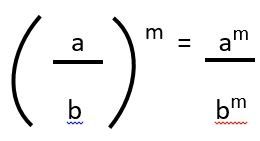
Contoh:
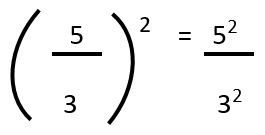
6. Pangkat Negatif
Pada sifat ini, jika (an)di bawah itu positif, maka saat dipindahkan ke atas menjadi negatif. Begitu juga sebaliknya, jika (an) di bawah itu negatif, maka saat dipindahkan ke atas menjadi positif. Kita lihat rumus dan contohnya ya.
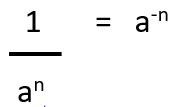
Contoh:
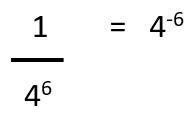
7. Pangkat Pecahan
Pada sifat ini, kamu bisa lihat, terdapat akar n dari am. Nah, ketika diubah jadi eksponen, akar n menjadi penyebut dan pangkat m menjadi pembilang, dengan syarat nilai n harus lebih besar atau sama dengan dua (n ≥ 2). Kita lihat rumus dan contohnya ya.
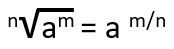
Contoh:
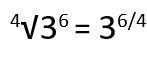
8. Pangkat Nol
a0 = 1. Untuk sifat yang satu ini, syaratnya nilai a tidak boleh sama dengan 0 ya, karena kalo a = 0, maka hasilnya tidak terdefinisi. Mau tau kenapa bisa gitu? Simak penjelasannya di video belajar ruangguru pada topik bilangan berpangkat kelas 9!
Nah, ke-8 sifat eksponen di atas harus kamu pahami benar-benar ya, karena seringkali dalam satu buah soal eksponen, terdapat banyak sifat eksponennya. Kalau kamu nggak benar-benar paham, kamu akan sangat kebingungan dalam mengerjakannya. Oke, sekarang kita coba mengerjakan sebuah soal ya!
Contoh Soal Eksponen
1. (6a3)2 : 2a4 = …
Penyelesaian:
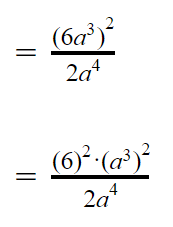
Di sini kamu lihat ya kalo (a3)2 itu merupakan bilangan berpangkat yang dipangkatkan lagi. Jadi, berdasarkan sifat eksponen poin 3, kita bisa kalikan pangkatnya.
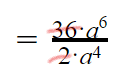
Kemudian, pangkat 6 bisa dikurangi dengan pangkat 4 karena merupakan operasi pembagian dengan basis yang sama. Jadi, jawabannya:
= 18a2 (Jawaban)
—
Sekarang sudah jelas kan, untuk memahami eksponen, kita harus mengerti sifat-sifat eksponennya. Kenapa begitu? karena untuk lanjut ke pembahasan selanjutnya, kita harus paham dulu dasarnya.

