Pengertian Eksponen
Eksponen atau biasa disebut bilangan berpangkat adalah bentuk perkalian bilangan dengan bilangan yang sama secara berulang-ulang. Misalnya perkalian bilangan 2 dengan dirinya sendiri sebanyak tiga kali, yaitu 2 × 2 × 2. Jika dinyatakan dalam bentuk eksponen, perkalian itu bisa ditulis menjadi 23. Pangkat tiga menunjukkan banyaknya pengulangan angka yang dikali. Adapun bentuk umum eksponen adalah sebagai berikut.
an dengan syarat a ≠ 1 dan n ∈ R
Keterangan:
a biasa disebut sebagai bilangan pokok atau basis; dan
n disebut sebagai eskponen atau pangkat.
Dari bentuk umum di atas diperoleh kesimpulan bahwa bilangan yang dipangkatkan (basis) tidak boleh bernilai satu dan pangkatnya masih termasuk anggota himpunan bilangan real. Mengapa basis tidak boleh satu? Karena berapapun pangkatnya jika basisnya satu maka hasilnya akan selalu satu.
Sifat-Sifat Eksponen
Setelah Quipperian tahu apa itu eksponen, kini saatnya belajar sifat-sifat apa saja sih yang berlaku pada operasi eksponen?
Sifat Operasi Penjumlahan Pangkat
Sifat pertama ini berlaku untuk penjumlahan pangkat pada dua atau lebih bilangan eksponen, bukan penjumlahan antarbilangannya ya. Jika dua atau lebih bilangan eksponen kamu kalikan, maka kamu bisa menjumlahkan pangkatnya dengan syarat basis bilangannya harus sama. Jika basisnya tidak sama, kamu tidak bisa menjumlahkan pangkatnya. Perhatikan bentuk di bawah ini:
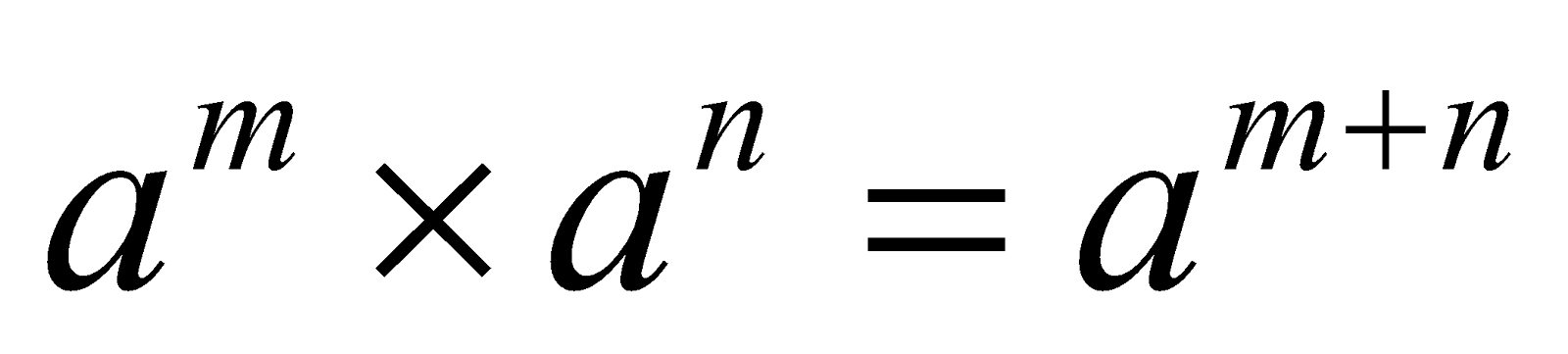
Contohnya, 53 × 54 = 53+4 = 57.
Untuk memudahkanmu ingat pernyataan “mengalikan bilangan berpangkat dengan bilangan pokok dasar yang sama, sama artinya dengan menjumlahkan pangkatnya”.
Sifat Operasi Pengurangan Pangkat
Pada prinsipnya, sifat operasi pengurangan pangkat sama seperti penjumlahan pangkat. Jika penjumlahan pangkat berlaku untuk perkalian dua atau lebih eksponen, maka pada pengurangan berlaku pembagian dua atau lebih eksponen. Jika kamu membagi dua bilangan eksponen dengan basis yang sama, sama artinya dengan mengurangi pangkatnya. Simak bentuk pengurangan pangkat berikut ini.
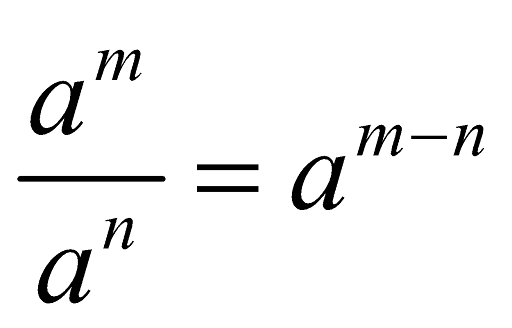
Contohnya, 29/23 = 29-3 = 26
Apabila nilai m = n, maka hasilnya pasti sama dengan satu. Apa benar demikian? Buat PR, ya!
Sifat Operasi Perkalian Pangkat
Perkalian antarpangkat bilangan eksponen berlaku jika kamu memangkatkan suatu bilangan eksponen. Bingung? Yuk, simak bentuk perkaliannya.
(am)n = am x x = amn, dengan syarat a ≠ 0 (basis tidak boleh sama dengan nol)Contoh, (34)2 = 34 × 2 = 38
Sifat Operasi Pembagian Pangkat
Jika operasi perkalian pangkat bisa diperoleh dengan mempangkatkan bilangan ekponen, lalu bagaimana dengan sifat operasi pembagian ya? Pembagian pangkat pada bilangan eksponen merupakan bentuk lain dari bilangan yang diakarkan. Penasaran? Yuk, simak berikut ini.
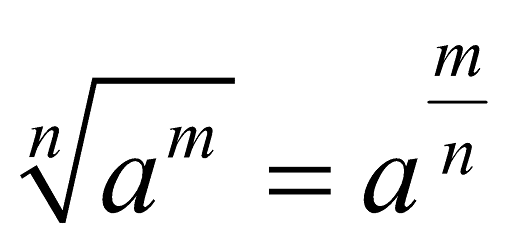
Dari bentuk di atas, Quipperian bisa tahu jika bilangan yang diakarkan itu sebenarnya bilangan eksponen yang pangkatnya berupa pecahan.
Sifat Pangkat Nol
Ada kalanya Quipperian menjumpai bentuk bilangan eksponen yang berpangkat nol. Lalu, apa arti pangkat nol itu? Ingat ya, berapapun bilangan jika dipangkatkan nol, maka hasilnya sama dengan satu. Adapun bentuk pangkat nol adalah a0 = 1, dengan syarat a ≠ 0. Contoh 20 = 1, 1.0000 = 1, 30 = 1, dan seterusnya.
Sifat Pangkat Bilangan Negatif
Lalu, bagaimana bentuk penyelesaian bilangan eksponen yang pangkatnya berupa bilangan bulat negatif? Bentuk perpangkatan dengan bilangan bulat negatif adalah sebagai berikut.

dengan syarat basis tidak boleh sama dengan nol (a ≠ 0)
Dari bentuk di atas, diketahui bahwa bilangan eksponen dengan pangkat bilangan bulat negatif merupakan kebalikan atau invers dari bilangan eksponen pangkat positifnya. Bagaimana tahu jika keduanya saling berkebalikan? Hasil perkalian antara keduanya sama dengan satu.
Sifat Pangkat Satu
Jika suatu bilangan dipangkatkan satu, hasilnya pasti sama dengan bilangan itu sendiri. Itu artinya, berapapun basisnya jika pangkatnya satu pasti hasilnya basis itu sendiri. Perhatikan contoh berikut.
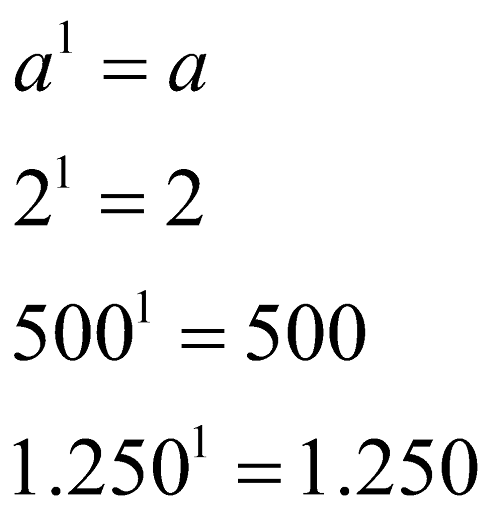
Bagaimana Quipperian? Mudah, kan?
Penerapan Sifat-Sifat Eksponen
Dalam kehidupan sehari-hari, sifat-sifat eksponen bisa dimanfaatkan untuk menyelesaikan berbagai permasalahan, contohnya seperti berikut.
Apakah Quipperian masih ingat, berapa kecepatan cahaya itu? Ya, benar sekali 300.000.000 m/s. Oleh karena kecepatannya cukup tinggi, maka kecepatan cahaya biasa dinyatakan dalam bentuk notasi ilmiah, yaitu 3 × 108 m/s. Jika ada benda lain selain cahaya yang kecepatannya 3 × 104 m/s, berapa perbandingan antara kecepatan cahaya dan kecepatan benda tersebut? Pada perbandingan ini, berlaku sifat operasi pengurangan pangkat ya.

Jadi, perbandingan kecepatan cahaya dan kecepatan benda tersebut adalah 104. Ternyata, dengan adanya sifat-sifat eksponen, kamu bisa lebih mudah menyelesaiakan soal-soal seperti contoh di atas ya.
Contoh Soal Sifat-Sifat Eksponen
Untuk mengasah pemahamanmu tentang pembahasan kali ini, yuk simak beberapa contoh soal berikut ini.
Contoh Soal 1
Sebuah toples memiliki ukuran panjang 25 cm dan lebar 5 cm. Berapakah luas toples tersebut dalam satuan km menggunakan sifat-sifat eksponen?
PEMBAHASAN
Diketahui:
p = 25 cm = 25 × 10-5 km
l = 5 cm = 5 × 10-5 km
Ditanya: L
Jawab:
Untuk mencari luas toples, gunakan persamaan luas persegipanjang ya.
Perhitungan di atas menunjukkan bahwa luas toples bisa dicari dengan sifat operasi penjumlahan pangkat. Sebelum mengoperasikan pangkat, tentukan dahulu bilangan-bilangan yang memiliki basis sama. Selanjutnya, operasikan pangkatnya sesuai sifat-sifat eksponen yang berlaku.
Jadi, luas toples dalam satuan km adalah 53 × 10-10 km.
Contoh Soal 2
Berapakah hasil dari 34040 + 92020?
Pembahasan:
Untuk menyelesaikan soal tersebut, gunakan sifat-sifat eksponen, ya.
Lakukan modifikasi kedua bilangan sedemikian sehingga keduanya memiliki basis dan pangkat yang sama seperti berikut.
34040 + 92020 = 34040 + (32)2020
= 34040 + 34040
= 2 × 34040Jadi, hasil dari 34040 + 92020 adalah 2 × 34040.

