TRIGONOMETRI

 

Pengertian Tabel Trigonometri

Tabel trigonometri adalah tabel yang berisi nilai trigonometri sudut-sudut istimewa. Sudut istimewa adalah sudut yang memiliki nilai trigonometri mudah untuk diingat dan dihafalkan. Oleh karena sudut memiliki rentang antara 0^o sampai 360^o, maka ada sifat pengulangan untuk sudut-sudut istimewa, misalnya nilai sin 30^o = sin 150^o = 0,5.

Nilai Trigonometri Berdasarkan Kuadran

Nilai trigonometri suatu sudut bergantung pada letak kuadrannya. Kuadran sudut dibagi menjadi empat, yaitu kuadran I, kuadran II, kuadran III, dan kuadran IV. Lalu, apa perbedaan kuadran-kuadran tersebut?

Kuadran I

Kuadran I terletak di antara sudut 0^o sampai 90^o. Di kuadran ini, semua nilai trigonometri akan bernilai positif, baik sinus α, cosinus α, maupun tangen α.

Kuadran II

Kuadran II terletak di antara sudut 90^o sampai 180^o. Di kuadran ini, hanya sinus α yang akan bernilai positif. Untuk cosinus α dan tangen α akan bernilai negatif. Contoh, sin 120^o=1/2√3 = 1/2 dan cos 120^o=-1/2

Kuadran III

Kuadran III terletak di antara sudut 180^o sampai 270^o. Di kuadran ini, hanya tangen α yang bernilai positif. Sementara cosinus α dan sinus α akan bernilai negatif.

Kuadran IV

Kuadran IV terletak di antara sudut 270^o sampai 360^o. Di kuadran ini, hanya cosinus α yang bernilai positif. Sementara sinus α dan tan α akan bernilai negatif.

Untuk lebih jelasnya, perhatikan letak kuadran berikut ini.

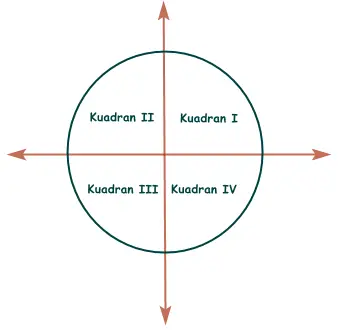
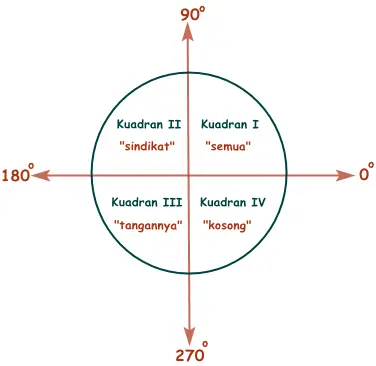
Agar lebih mudah dalam mengingat nilai trigonometrinya, gunakan SUPER “Solusi Quipper” berikut.

“SEMUA SINDIKAT TANGANNYA KOSONG”

Artinya: di kuadran I semua bernilai positif, di kuadran II hanya sin yang positif, di kuadran III hanya tan yang positif, dan di kuadran IV hanya cos yang positif.

Tabel Trigonometri Sudut Istimewa Lengkap

Mungkin kamu biasa mengenal sudut istimewa 0^o sampai 90^o. Tahukah kamu jika sudut istimewa itu tidak hanya terbatas sampai 90^o, namun sampai 360^o. Berikut ini akan disajikan tabel trigonometri sudut istimewa lengkap mulai 0^o sampai 360^o.

Tabel Trigonometri di Kuadran I (0^o – 90^o)

Sudut istimewa yang berada di kuadran I meliputi, 0^o, 30^o, 45^o, 60^o, dan 90^o. Adapun tabel trigonometri sudut istimewa di kuadran I adalah sebagai berikut.

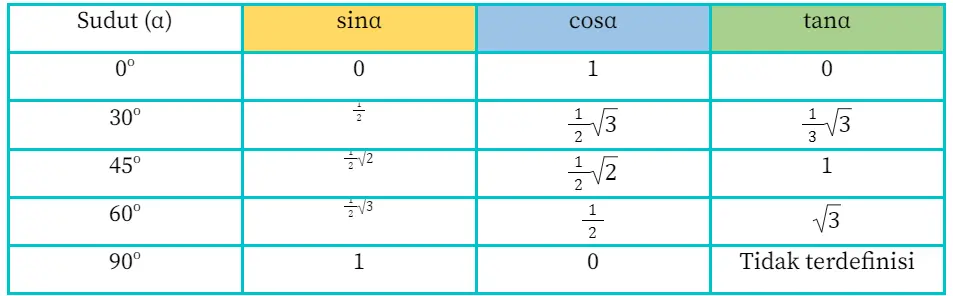
Tabel Trigonometri di Kuadran II (90^o – 180^o)

Sudut istimewa yang berada di kuadran II meliputi 90^o, 120^o, 135^o, 150^o, dan 180^o. Adapun tabel trigonometri sudut istimewa di kuadran II adalah sebagai berikut.

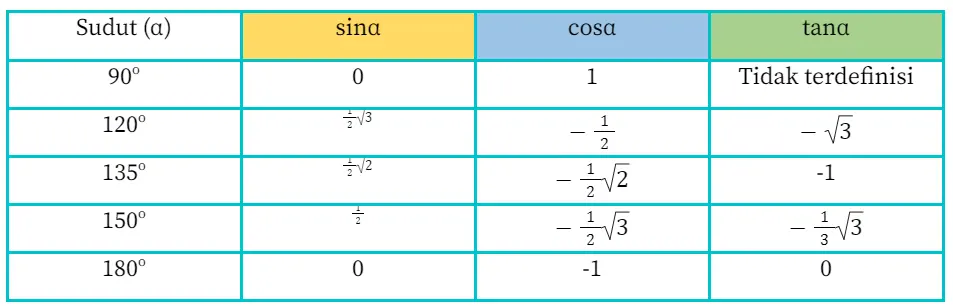
Tabel Trigonometri di Kuadran III (180^o – 270^o)

Sudut istimewa yang berada di kuadran II meliputi 180^o, 210^o, 225^o, 240^o, dan 270^o. Adapun tabel trigonometri sudut istimewa di kuadran III adalah sebagai berikut.

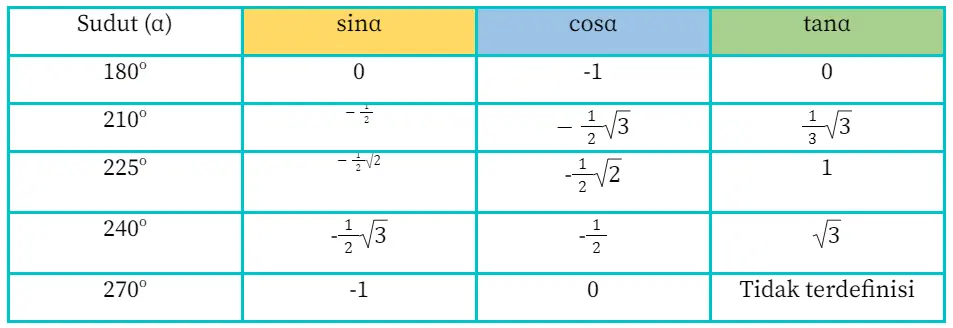
Tabel Trigonometri di Kuadran IV (270^o – 360^o)

Sudut istimewa yang berada di kuadran II meliputi 270^o, 300^o, 315^o, 330^o, dan 360^o. Adapun tabel trigonometri sudut istimewa di kuadran IV adalah sebagai berikut.

Baca Juga: Rumus Perbandingan Trigonometri, Sudut Istimewa pada Segitiga Siku Siku

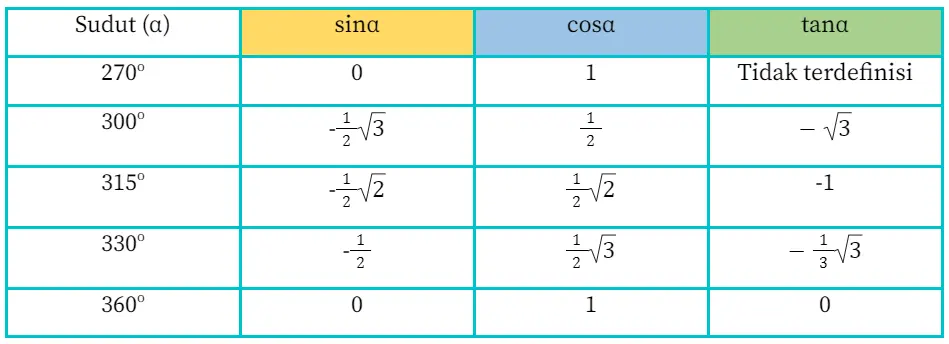
Persamaan Nilai Trigonometri Antar Kuadran

Dari tabel di atas, bisa disimpulkan bahwa sudut-sudut di setiap kuadran ada yang memiliki nilai trigonometri sama, misalnya sin 210^o = sin 330^o = -0,5, cos = 120^o = cos 240^o = -0,5. Dari kesamaan nilai-nilai tersebut, diperoleh suatu persamaan yang bisa memudahkanmu dalam menyelesaikan nilai trigonometri antarkuadran. Berikut ini persamaannya.

Persamaan Trigonometri di Kuadran I (0^o – 90^o)

Adapun persamaan yang berlaku pada trigonometri di kuadran I adalah sebagai berikut.

1. sin(90^o – α) = cosα
2. cos(90^o – α) = sinα
3. tan(90^o – α) = cotα

Perhatikan contoh berikut.

Buktikan bahwa nilai dari sin(90 – 30^o) = cos(30^o)

Pembahasan :

Dari persamaan sin(90^o – α) = -cosα, diperoleh :

sin(90 – 30^o) = cos(30^o)

↔ sin 60^o = cos 30^o

Untuk membuktikannya, lihat kembali tabel trigonometri!

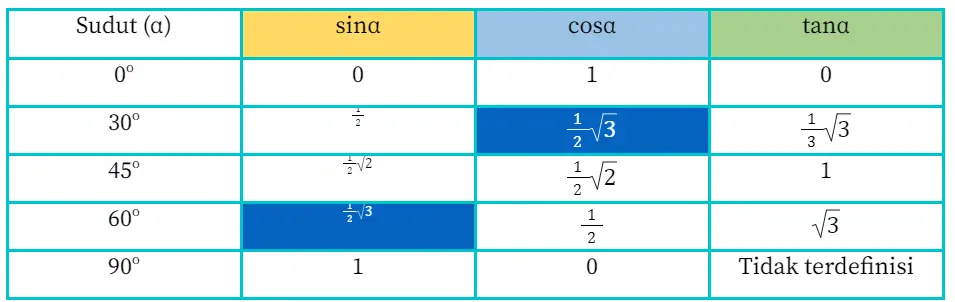
Coba kamu perhatikan sel yang diberi warna ungu. Dari situ, terlihat jika nilai sin(60^o)

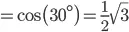
Persamaan Trigonometri di Kuadran II (90^o – 180^o)

Berdasarkan tabel, diperoleh hubungan bahwa sin(120^o) = sin(60^o), di mana 120^o + 60^o = 180^o. Dengan demikian, persamaan yang berlaku adalah sebagai berikut.

1. sin(180^o – α) = sinα
2. cos(180^o – α) = -cosα
3. tan(180^o – α) = -tanα

Perhatikan contoh berikut.

Buktikan bahwa cos(180^o – 45^o) = -cos(45^o)

Pembahasan :

cos(180^o – 45^o) = -cos(45^o)

↔ cos(135^o) = -cos(45^o)

↔ – 1/2√2 = -1/2 √2 (terbukti)

Persamaan Trigonometri di Kuadran III (180^o – 270^o)

Adapun persamaan trigonometri di kuadran III adalah sebagai berikut.

1. sin(180^o + α) = -sinα
2. cos(180^o + α) = -cosα
3. tan(180^o + α) = tanα

Persamaan Trigonometri di Kuadran IV (180^o – 270^o)

Untuk di kuadran IV, berlaku persamaan trigonometri sudut negatif sebagai berikut.

1. sin (360^o – α) = -sin α
2. cos (360^o – α) = cos α
3. tan (360^o – α) = -tan α

Mengapa sudutnya negatif? Karena sudut negatif diukur dari sumbu-x positif yang arahnya searah dengan putaran jarum jam.

Dengan adanya persamaan-persamaan di atas, kamu tidak perlu repot-repot menghafalkan semua nilai trigonometri mulai 0o sampai 360o, ya. Cukup pahami rumus dan letak kuadran sudutnya.

Baca Juga: Rumus Identitas Trigonometri, Contoh Soal dan Pembahasannya

Contoh Soal

Untuk mengasah kemampuanmu, yuk simak contoh soal berikut ini.

Contoh Soal 1

Jika sinx = sin(60^o) dengan 0^o ≤ x ≤ 360^o, tentukan sudut x yang memenuhi persamaan tersebut!

Pembahasan :

Di soal tertulis bahwa sinx = sin(60^o) dengan 0^o ≤ x ≤ 360^o. Artinya, solusi untuk sudut x hanya berada di kuadran I dan kuadran II. Mengapa demikian? Karena sinus bernilai positif di kuadran II. Dengan demikian, diperoleh dua solusi seperti berikut.

1. sinx = sin(60^o) → x = 60^o
2. sin(180^o – 60^o) = sin(60^o) → x = 120^o

Jadi, nilai sudut x yang memenuhi adalah {60^o, 120^o}.

Contoh Soal 2

Tentukan nilai trigonometri berikut ini.

1. tan(315^o)
2. sin(210^o)
3. cos(225^o)

Pembahasan :

Mula-mula, tentukan dahulu letak kuadran sudutnya. Lalu, gunakan persamaan trigonometri di setiap kuadrannya!

1. tan(315^o) → sudut 315^o berada di kuadran IV Persamaan yang berlaku adalah tan (360^o – α) = -tan α. Dengan demikian: tan(315^o) = tan(360^o – 45^o) tan(360^o – 45^o)= – tan(45^o) = -1 Jadi, tan(315^o) = -1.
2. sin(210^o) → sudut 210^o berada di kuadran III Persamaan yang berlaku adalah sin(180^o + α) = -sinα. Dengan demikian: sin(210^o) = sin(180^o + 30^o) ↔ sin(180^o + 30^o) = -sin(30^o) = -1/2 Jadi, sin(210^o) = -1/2
3. cos(225^o) → sudut 225^o berada di kuadran III Persamaan yang berlaku adalah cos(180^o + α) = -cosα. Dengan demikian: cos(225^o) = cos(180^o + 45^o) ↔ cos(180^o + 45^o) = -cos(45^o) = -1/2√2 Jadi, cos(225^o) = -1/2√2.